Isabela de Paula Salgado holds a B.S (2016) and a M.Sc. (2019) in Civil Engineering from PUC-Rio.  She is currently part of a Joint PhD Programme between UNU-FLORES and Technische Universität Dresden, where she is a member of the GRK 2250 Research Training Group. Her current project is focused on the sustainability and resilience assessments of novel mineral-bonded composites.

 

isabela.depaulasalgado@tu-dresden.de/ dpsalgado@unu.edu

Flavio de Andrade Silva holds a B.S. in Civil Engineering from PUC-Rio (2001), a M.Sc. in Civil Engineering from PUC-Rio (2004), a Ph.D. in Civil Engineering from UFRJ (2009) and a Postdoctoral Fellowship at the Technische Universität Dresden (2010). He is currently a professor at the civil engineering department of PUC-Rio. He has experience in Civil Engineering, with emphasis on Composite Materials. He is a member of the Technical Committee ACI 544, Rilem TC-TRC and Rilem TC-HFC.

 

fsilva@puc-rio.br

In recent years, there has been an increasing interest in sustainable materials, particularly renewable and biodegradable resources. Literature works indicate the potential of natural fibers to replace their synthetic counterparts, as they are generally light and thermally insulating, with high tensile strength and stiffness [1,2]. Such is the case of natural fiber reinforced composites in comparison to glass and polypropylene fiber-reinforced alternatives, since the first provides comparable performance but with enhanced absorption capacity and reduced pollutant emissions [3,4]. Natural reinforcement can improve the material's ductility and post-cracking toughness [5]. The performance efficiency depends on the fiber morphology, orientation, and quantity; fiber-matrix interface; stress transfer between matrix and reinforcement [6]. On that account, the matrix's strain capacity is lower than the fiber's, so it fails before the reinforcement's total capacity is reached. The fibers then intersect the cracks, contributing to the material's energy dissipation via pull-out and debonding [7].

Curauá (Ananas erectifolius) stands out among traditional Brazilian fibers due to its superior tensile strength compared to sisal, jute, and coir [5,6]. Curauá fibers are also cheaper than flax, polypropylene, and glass fibers [10]. Several studies present good results with Curauá reinforced composites, owing to their ductility and post-cracking strength [7,8] – as is the case of Strain-Hardening Cementitious Composites (SHCC), which are reportedly suitable for facades, repair, and structural uses [12,13].

Using a cementitious matrix with natural fibers as reinforcement, however, demands additional measures to protect the composite's integrity. The cement paste has a negative effect on the fibers, presumably leading to early loss of composite strength, as demonstrated by several research findings [9,10]. Surface treatments on fibers can change their water absorption capacity and improve their compatibility with the matrix [15,16]. Partially replacing cement with pozzolanic materials has also proven effective in terms of durability [11,12] and sustainability issues related to CO₂ emissions and other greenhouse gases [20, 21].

Additionally, materials with thermal insulation properties are recommended to reduce gas emissions and the need for refrigeration systems. AAC is one of the options as it has a high thermal insulation capacity due to its low specific weight and conductivity coefficient ranging between 0.1 and 0.22 W/mK (for densities between 300 and 700 kg/m³) [5]. Several studies have been conducted on the thermal performance of cellular concrete [6-8] and its moisture variation is said to influence its thermal conductivity more than temperature increase: the higher the moisture content, the greater the heat conduction capacity [9,10]. Its production techniques are more energy-efficient and require fewer primary resources, resulting in lower gas emissions (CO₂, CO, NO_x) when compared to other standard industrial processes [22]. AAC is lightweight, isotropic, and recyclable [15,17,18].

The material’s high porosity is responsible for its low specific weight and good thermal performance [14–16], but also compromises its compressive strength and, consequently, possible structural applications. The industry's need for new high-performance materials is met by sandwich structures. Sandwich panels are usually light, stiff, and easy to manufacture [28]. Sandwich panels with thin ductile layers and a thermal core allow for efficient structural, acoustic, and thermal building systems [29].

This study proposes a solution that combines sustainability and mechanical performance: sandwich panels with natural fiber-reinforced composite layers for ductility and resistance, and an AAC core for insulation. Panels and composites were tested in monotonic four-point bending. The sandwich panels were also subjected to cyclic bending tests to investigate the mechanisms of degradation and energy loss. We calculated flexural strength and toughness, and studied failure mechanisms. SEM, optical microscopy, and pull-off tests were used to evaluate the AAC-composite laminate bond.

Experimental Program

Materials and Panels Production

The Curauá fibers used in this work come from the Ananas comosus erectifolius plant, whose leaves were obtained from a plant farm in Aurora do Pará, Brazil. To be employed as reinforcement, the fibers had to be cleaned for an hour in hot water (70-80°C) followed by 48 hours of natural drying. The dry fiber bundles were meticulously brushed into filaments, which were then divided into 350 mm layers. Martel et al. [17] describe in detail the microstructure, water absorption capacity, and mechanical performance of the fibers employed in this technique. The curauá filaments have a tensile strength of 872 (326) MPa and a Young's modulus of 16.5 (5.7) GPa.

In addition to Lafarge-CPV-ARI Holcim's Brazilian Portland cement, Metacaulim do Brasil Indstria e Comércio Ltda's Metakaolin (MK) were used in the composite matrix. The components were blended 1:1:0.4 (binder: sand: water), with the binder (cementitious materials) being 50% Portland cement, 40% MK, and 10% fly ash. The use of pozzolanic elements in the mix design lowered the calcium hydroxide content, enhancing the fiber durability in the cementitious matrix. The appropriate workability of the matrix was achieved by adding 2.5 % superplasticizer Plastol 4100 to the binder weight, which delivered 400 mm of slump flow according to ASTM C230/C230M [30]. The resultant matrix displayed 74 MPa of compressive strength.

Sandwich panels of 350 x 60 x 90 mm (length x width x thickness) were produced, consisting of two fiber-reinforced composite layers of 10 mm each and a 70 mm thick precast AAC core. Lightweight AAC blocks were provided by Precon.

In a planetary mixer, the sand and cementitious ingredients were first combined with water for 1 min 30 s. After homogenization, the superplasticizer was applied gradually and mixed for 4 minutes. Before molding, the curauá fibers were brushed, split into bundles, trimmed to length, and then weighted.  The bundles were then submerged for 2 hours to achieve saturation and avoid volumetric differences when placed in the matrix. After drying, each fiber layer was brushed again to ensure proper reinforcement alignment in the matrix.

Composites of 350 mm x 60 mm x 10 mm (length x width x thickness) were produced by hand casting long unidirectional curauá fibers (7.5% volume proportion). The three layers had the same approximate weight (4.2-5 g). The laminates were then cast directly on the AAC blocks, which had been moistened to avoid water absorption during the initial mortar layer. The outer layers were cast individually, taking two days to be produced. The panels were then demolded and cured for 28 days in a humid chamber. No interlayer connectors were employed, the composite-core adhesion was dependent on the cement and AAC's porous surface.

Testing

·       AAC Characterization tests

In accordance to ASTM C1693 (2009), the compressive strength of AAC must be evaluated in three cubic specimens of 100 mm edge, extracted by dry cutting and conditioned to a moisture content between 5 and 15% by mass. In order to reach the desired content, the cubic samples were dried in an oven at a temperature of 70ºC, requiring approximately 24 hours to reach the desired humidity range. The block moisture content is considered as the average of the values ​​obtained from the three specimens analysed. After conditioning, the specimens had an average moisture content of 11.7 (±0.4) % before the compression test. The specimens were tested in a Controls C46Z00 compression machine, half of the maximum load foreseen at 0.03 MPa/s was applied, with the remainder of the load being applied at 0.015 MPa/s until failure. The test speed was defined based on the moment of failure, between 1 and 2 minutes after the beginning of the test, as recommended by the standard.

·       Monotonic four-point bending tests

The mechanical characterization of the sandwich panels and their components, i.e. the layers and core, was focused on the flexural response of the specimens. Four-point bending tests are particularly suitable for sandwich structures since they evaluate how the materials influence their overall performance [11]. Three sandwich panels were tested on a MTS 204.63 with load capacity of 100 kN. A constant span of 270 mm and a distance of 90 mm between the load points were established for the panels during testing. Two displacement transducers, placed at mid-span, measured the vertical displacement of the specimens. The bending tests were performed under displacement control rate of 1 mm/min. Figure 1-a illustrates the test set-up.

Three AAC blocks were tested on a MTS 204.63 under displacement control of 0.1 mm/min, with a span length of 225 mm. Mid-span deflections were measured using two transducers, as demonstrated in Fig. 2-b. The experiment was executed in accordance to the BS EN 1351 standard [12].

The flexural behavior of eight composites was assessed according to the ASTM C1341 [13]. The laminates were tested on a MTS 810 with load capacity of 500 kN. A load cell of 2.5 kN was attached to the system.  Two transducers, located on the upper surface of the composite, measured the vertical displacement of the specimens (Fig. 2-c). The test was carried under a displacement rate of 1mm/min, with a span length of 270 mm.

Results

The mechanical behavior of the specimens tested under four-point bending is summarized in Tab.1, where the average values of strength, maximum deflection and toughness are presented. The typical flexural response of the AAC blocks and the composites is shown in Fig. 3.

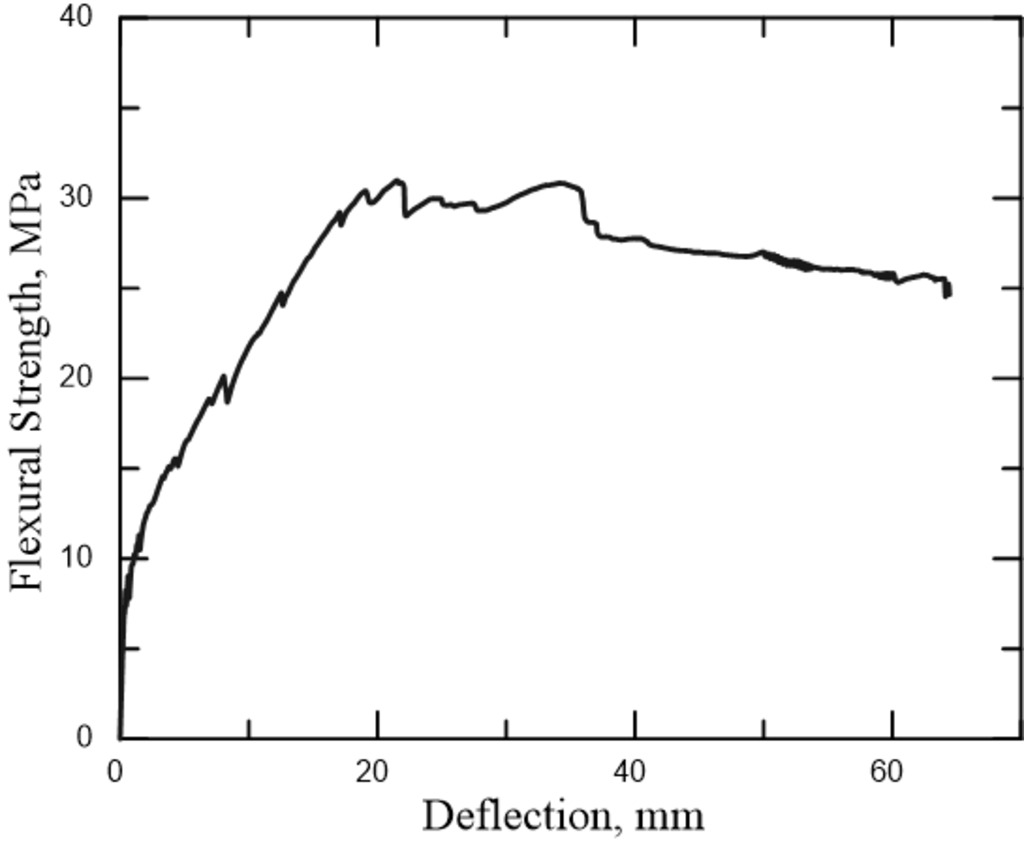
Figure 3-a shows the average response of the AAC blocks, which exhibited a brittle failure at mid-span after the maximum force. In general, the material did not prevent the formation and propagation of cracks. The flexural strength of the test specimens was calculated according to Eq. (1):

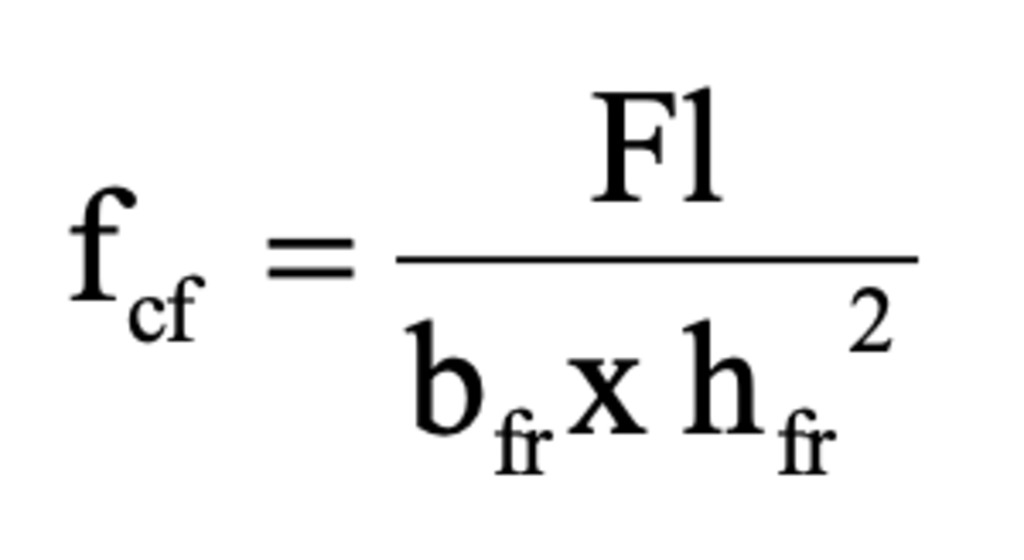
Where f_cf  is the flexural strength, F is the maximum load, l is the span length, b_fr and h_fr are the cross-sectional dimensions (width and height) of the specimens at the location of fracture. The values were expressed to the nearest 0.1 MPa.

The test specimens achieved an average value of 0.72 MPa of flexural strength, with corresponding maximum deflection of 0.48 mm and 0.25 J of toughness. In general, the strength of AAC is inherently associated with its density and inversely proportional to it [14]. Analogous values can be found in literature: Dey et al. [15] obtained 1.1 MPa of strength and 0.31 mm of maximum deflection in three-point bending tests for AAC blocks with 250 mm x 50 mm x 50 mm (length x width x thickness).  Similarly, Bonakdar et al. [16] achieved 0.66 MPa of flexural strength deflection in three-point bending tests for notched specimens with 500 mm x 150 mm x 150 mm (length x width x thickness).

Figure 3-b represents the stress-deflection correlation displayed by the composites tested under bending.  The cracking mechanism can be interpreted through different regions based on the composite’s typical response, as demonstrated by works of literature such as Mobasher et al. [17], Silva et al. [18] and Yao et al. [19]. Initially, a linear-elastic behavior is observed between matrix and fibers until approximately 10 MPa. Subsequently, after the first crack is formed, other cracks initiate and propagate across the composite; after stabilization of the cracking range, there is a substantial decrease of the spacing between cracks, which leads to their progressive widening. The load-carrying capacity of the specimen decreases until rupture. In general, each region relies on a certain component: the first zone depends on the matrix, while the latter is governed by the reinforcement performance and its ability to control crack distribution.

The flexural properties of the composites can be calculated using classic beam equations, which assume that the material is homogeneous, linear-elastic and its sections remain plane after bending.  The average flexural strength of the material, 32.16 MPa, as well as its toughness at peak load, 13.32 J, are similar to other values found in literature for cementitious composites: Silva et al. [18] obtained 29 MPa of strength and 22 KJ/m² of toughness for sisal textile-reinforced composites with 10% of volume fraction. The work of d’Almeida et al. [20] tested composites with five layers of curauá and 6% of volume fraction, achieving 27.52 MPa and 29.13 kJ/m², respectively. Specimens with three layers of long fibers of curauá were tested under four-point bending by Souza et al. [21] exhibiting 28 MPa and 16.4 J. These values are consistent with a ductile behavior and a satisfactory mechanical performance.

The three-layered composites presented a deflection hardening behavior and multiple crack formation, which indicates a high energy absorption capacity. The predominant mode of failure was characterized by the formation of cracks on the bottom surface (region under tension), which propagated across the width of the material. Since the fibers reinforce the direction parallel to the layers, the composite must rely on the matrix, a fragile element, to resist the transverse stresses – hence resulting on the observed crack pattern.

According to Daniel & Abot [22] the structural performance of sandwich panels does not rely exclusively on the materials properties and their bond, but also on the non-linear behavior of the elements, the loading conditions and the failure mechanisms of the structure. The behavior of a sandwich panel is frequently compared to an I-beam, where the layers are homologous to the flanges, carrying the normal stresses, while the core is equivalent to the web, resisting the shear stresses [23]. This separation between the composite layers by the core also contributes to a higher moment of inertia. Ordinary beam theory can be used to explain the mechanical behavior of sandwich panels by approximating the stresses and deflections of the structure to conventional bending equations [24].

The panels’ mechanical properties were calculated with Allen’s [24] equations and the standards ASTM D7249 [25] and ASTM D7250 [26]. The rigidity of a sandwich beam is given by D, represents the sum of the flexural rigidities of each constituent, skins and core, measured about the centroidal axis of the cross-section. If the ratio between the distance d between the centroids of both facings and the face thickness t is higher than 5.77 (d/t > 5.77), it can be rewritten as:   

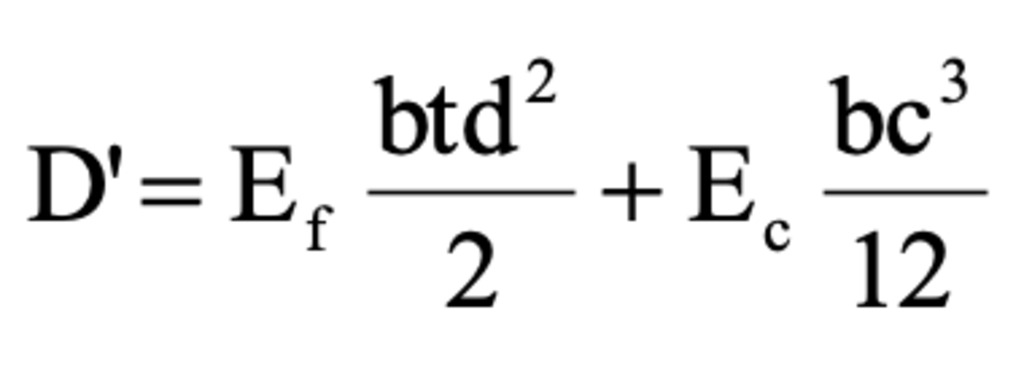
Using ASTM D7250 [26], it is possible to calculate the sandwich panels' transverse shear rigidity.

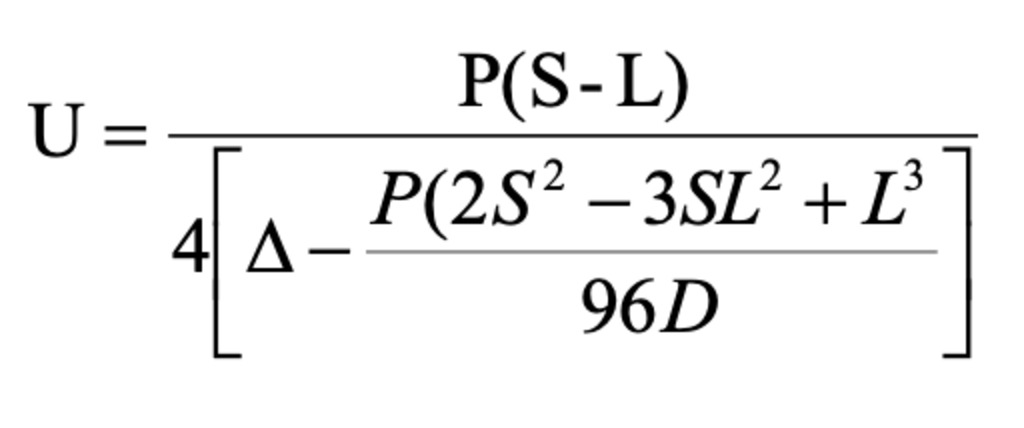
Where U is the transverse shear rigidity, P is the total applied force, S is the support span length, L is the load span length, Δ is the beam mid-span deflection, and D is the flexural rigidity, previously calculated. 

The shear rigidity was calculated for each tested panel for a series of forces (P), with their respective deflections (Δ), up to the point of the maximum applied load (P_max). These values have to be calculated for a minimum of 10 force levels evenly spaced along the force-deflection curve. An interval of 0.05 mm was established between each force applied in the formula up to the peak load. The average value of the panels' transverse shear rigidity U is 2.29 x 10⁵ N.

Table 1: Mechanical properties of the tested sandwich panels under monotonic bending tests

The flexural properties and load-carrying capacity of the test specimens proved to be equivalent to sandwich panels with similar structures. Three-point bending experiments were performed by Dey et al. [15] on sandwich panels with 250 mm x 50 mm x 100 mm (length x width x thickness) with two layers of alkali resistant glass (ARG) textiles and an AAC core; the specimens exhibited 2.4 MPa of flexural strength and 1.34 mm of deflection at peak load. Frazão et al. [11] developed panels with outer layers of sisal fiber-cement composites and a core layer of polypropylene fiber-reinforced lightweight concrete, obtaining maximum load of 18 kN and 11 mm of deflection. In this case, the fiber-reinforced core allowed the specimens to achieve a higher strength, while the long sisal fibers assured the multiple cracking behavior of the composites.

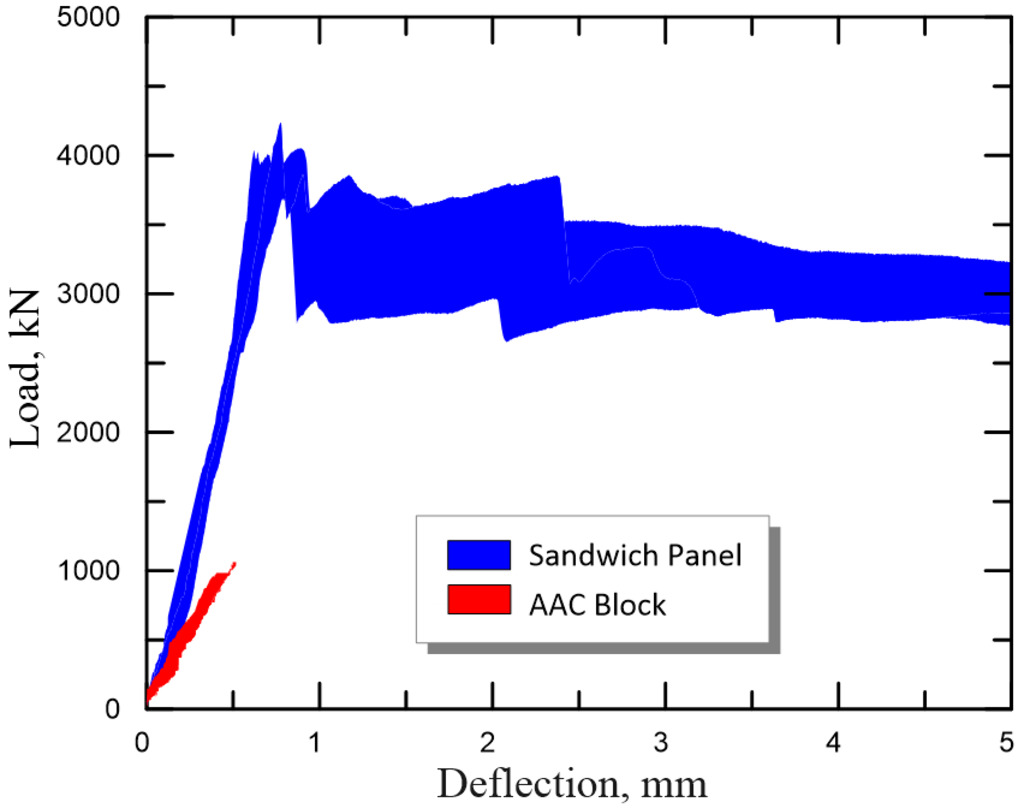
Figure 4 shows the load-deflection curves of each panel, as well as the contrast between the behavior of the material and plain AAC blocks. The performance improvements derived from the sandwich structure, not only in flexural strength but also in energy absorption capacity, are noteworthy: the toughness was increased by a factor of 7 for the sandwich panels at the maximum load in comparison to the AAC blocks. This response is justified by the fiber-reinforced composites and the adequate bonding between composite layers and core, which provided a better distribution of cracks and a ductile behavior. Overall, the test specimens demonstrated an increase in flexural strength and toughness up until the peak load (usually around 4 kN), after which, despite the gradual loss of load-carrying capacity, the material exhibited a satisfactory deflection capacity.

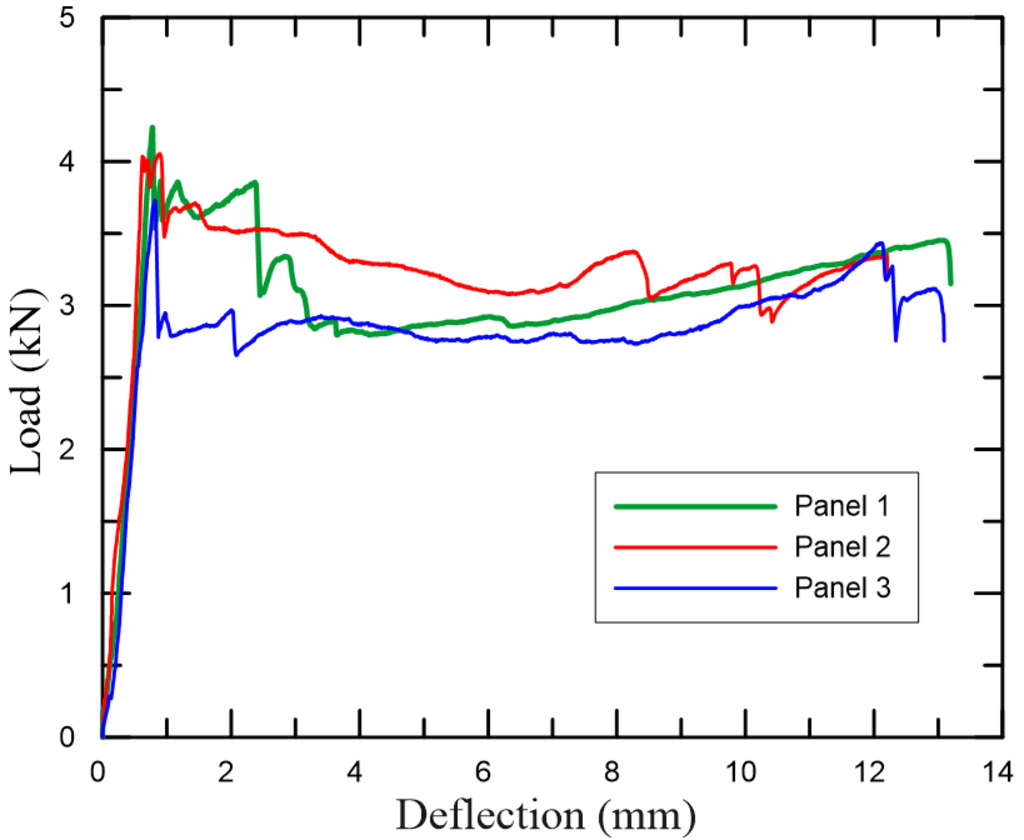
The mode of failure of the tested sandwich panels was predominantly due to shear cracks at the core, which propagated from the loading bars to the supports. The AAC, in special, demonstrated a different behavior when tested as isolated element, with a brittle failure and a major crack in the mid-span (Fig. 5-b); in contrast, when the material acted as a core (bonded with the laminate composites), it presented transverse cracks and a more ductile behavior (Fig. 5-c).

 Conclusions

The curauá unidirectional fibers were particularly suitable as reinforcement of the cementitious composites since the fabric provided strength and toughness improvements in the post-cracking behavior of the material. All of the tested laminar composites presented multiple cracking and deflection hardening behavior. The AAC core, given its low compressive strength and brittle failure, showed a higher ductility when supported by the composites in the sandwich structure. In general, the development of such sandwich panels provided a better strength/weight ratio and a higher energy absorption. The deflection softening behavior displayed by the panels under bending revealed a satisfactory ductility and allowed a gradual energy dissipation.

References

[1]       S. N. Monteiro, F. P. D. Lopes, A. P. Barbosa, A. B. Bevitori, I. L. Amaral Da Silva, and L. L. Da Costa, “Natural lignocellulosic fibers as engineering materials- An overview,” Metall. Mater. Trans. A Phys. Metall. Mater. Sci., vol. 42, no. 10, 2011, doi: 10.1007/s11661-011-0789-6.

[2]       D. B. Dittenber and H. V. S. Gangarao, “Critical review of recent publications on use of natural composites in infrastructure,” Compos. Part A Appl. Sci. Manuf., vol. 43, no. 8, pp. 1419–1429, 2012, doi: 10.1016/j.compositesa.2011.11.019.

[3]       S. V. Joshi, L. T. Drzal, A. K. Mohanty, and S. Arora, “Are natural fiber composites environmentally superior to glass fiber reinforced composites?,” 2004, doi: 10.1016/j.compositesa.2003.09.016.

[4]       R. D. S. G. Campilho, Natural fiber composites. 2015.

[5]       RILEM Recommended Practice, Autoclaved Aerated Concrete: Properties, Testing and Design. London, UK: E & FN SPON, 1993.

[6]       D. Gawin, J. Kosny, and K. Wilkes, “Thermal Conductivity of Moist Cellular Concrete—Experimental and Numerical Study,” Am. Soc. Heating, Refrig. Air-Conditioning Eng., no. May, 2004, [Online]. Available: http://www.ornl.org/sci/roofs+walls/staff/papers/new_90.pdf.

[7]       H. Q. Jin, X. L. Yao, L. W. Fan, X. Xu, and Z. T. Yu, “Experimental determination and fractal modeling of the effective thermal conductivity of autoclaved aerated concrete: Effects of moisture content,” Int. J. Heat Mass Transf., 2016, doi: 10.1016/j.ijheatmasstransfer.2015.08.103.

[8]       A. D. Stuckes and A. Simpson, “The effect of moisture on the thermal conductivity of aerated concrete,” Build. Serv. Eng. Res. Technol., vol. 6, no. 2, pp. 49–53, 1985, doi: 10.1177/014362448500600201.

[9]       M. Jerman, M. Keppert, J. Výborný, and R. Černý, “Hygric, thermal and durability properties of autoclaved aerated concrete,” Constr. Build. Mater., vol. 41, pp. 352–359, 2013, doi: 10.1016/j.conbuildmat.2012.12.036.

[10]     C. LAURENT, JP; GUERRE-CHALEY, “Influence of water content and temperature on the thermal conductivity of autoclaved aerated concrete,” Mater. Struct., vol. 28, pp. 464–472, 1995.

[11]     C. Frazão, J. Barros, R. Toledo Filho, S. Ferreira, and D. Gonçalves, “Development of sandwich panels combining Sisal Fiber-Cement Composites and Fiber-Reinforced Lightweight Concrete,” Cem. Concr. Compos., vol. 86, pp. 206–223, 2018, doi: 10.1016/j.cemconcomp.2017.11.008.

[12]     British Standards, “BS EN 1351 - Determination of flexural strength of autoclaved aerated concrete,” British-Adopted Eur. Stand., 1997.

[13]     AMERICAN SOCIETY FOR TESTING AND MATERIALS, “ASTM C1341-13 - Standard Test Method for Flexural Properties of Continuous Fiber-Reinforced Advanced Ceramic Composites,” ASTM Int., vol. i, pp. 1–21, 2013, doi: 10.1520/C1341-13.2.

[14]     RILEM, Autoclaved Aerated Concrete: Properties, Testing and Design. E&FN Spon, 1993.

[15]     V. Dey, G. Zani, M. Colombo, M. Di Prisco, and B. Mobasher, “Flexural impact response of textile-reinforced aerated concrete sandwich panels,” Mater. Des., vol. 86, pp. 187–197, 2015, doi: 10.1016/j.matdes.2015.07.004.

[16]     A. Bonakdar, F. Babbitt, and B. Mobasher, “Physical and mechanical characterization of Fiber-Reinforced Aerated Concrete (FRAC),” Cem. Concr. Compos., vol. 38, pp. 82–91, 2013, doi: 10.1016/j.cemconcomp.2013.03.006.

[17]     B. Mobasher, J. Pahilajani, and A. Peled, “Analytical simulation of tensile response of fabric reinforced cement based composites,” Cem. Concr. Compos., 2006, doi: 10.1016/j.cemconcomp.2005.06.007.

[18]     F. de A. Silva, B. Mobasher, and R. D. T. Filho, “Cracking mechanisms in durable sisal fiber reinforced cement composites,” Cem. Concr. Compos., vol. 31, no. 10, pp. 721–730, 2009, doi: 10.1016/j.cemconcomp.2009.07.004.

[19]     Y. Yao, F. A. Silva, M. Butler, V. Mechtcherine, and B. Mobasher, “Tension stiffening in textile-reinforced concrete under high speed tensile loads,” Cem. Concr. Compos., 2015, doi: 10.1016/j.cemconcomp.2015.07.009.

[20]     A. L. F. S. D’Almeida, J. A. Melo Filho, and R. D. Toledo Filho, “Use of curaua fibers as reinforcement in cement composites,” 2009, doi: 10.3303/CET0917287.

[21]     L. O. Souza, L. M. S. Souza, and F. A. Silva, “Mechanics and cracking mechanisms in natural curauá textile reinforced concrete,” RILEM Bookseries, 2018, doi: 10.1007/978-94-024-1194-2_42.

[22]     I. M. Daniel and J. L. Abot, “Fabrication, testing and analysis of composite sandwich beams,” Compos. Sci. Technol., 2000, doi: 10.1016/S0266-3538(00)00039-7.

[23]     D. ZENKERT, An Introduction to Sandwich Construction. Engineering Materials Advisory Services Ltd., 1995.

[24]     H. D. Allen, Analysis and Design of Structural Sandwich Panels. Pergamon Press, 1969.

[25]     American Society for the Testing of Materials, “ASTM D7249: Standard Test Method for Facing Properties of Sandwich Constructions by Long,” Annu. B. ASTM Stand., vol. i, pp. 1–9, 2006, doi: 10.1520/D7249.

[26]     American Society for the Testing of Materials, “ASTM D7250: Standard Practice for Determining Sandwich Beam Flexural and Shear Stiffness,” ASTM Stand., vol. i, pp. 1–8, 2009, doi: 10.1520/D7250.