Lorenzo Miccoli is since 2017 project leader at the Xella Technologie- und Forschungsgesellschaft mbH. He was a Research Associate at the Bundesanstalt für Materialforschung und -prüfung (BAM) from 2011 to 2017. He received his PhD in Building Engineering at the University of Rome ‘Tor Vergata’. He is a visiting researcher at the University of South Carolina in 2016 and at the Yangzhou University in 2005. He is a member of the CEN TC 250/SC6.PT2 for the revision of the Eurocode EN 1996-1-2. His main research focuses on mechanical characterisation of masonry, finite element modelling, seismic and fire resistance, dynamic and static analysis of buildings. He is the author of more than 80 scientific publications in the field of material testing and structural safety.

lorenzo.miccoli@xella.com

 

Marco Andreini holds a PhD in Structural Engineering, collaborating with Studio Masiello Strutture (Pisa, Italy) consulting company. He is a member of the CEN TC 250/SC6.PT2 for the revision of the Eurocode EN 1996-1-2. In parallel, he is responsible for the Structural Safety Expertise Service of the Occupational Health and Safety and Environmental Protection Unit of the European Organisation for Nuclear Research (CERN). He is involved in all the main CERN projects such as High Luminosity Large Hadron Collider (HL-LHC), Future Circular Collider (FCC), etc. He recently joined the Expert Network on Design of Underground Structures managed by the Joint Research Centre (JRC) of the European Commission. He is the author of more than 50 scientific publications in the field of structural safety.            

marcoandreini@smstrutture.it

The current version of EN 1996-1-2 [1, 2] offers only tabulated data as a reliable method for structural fire assessment of masonry walls. The current Annex C presents an assessment method of masonry piers based on the definition of parts of the cross-section with reduced and zero resistance due to the rise in temperature. The current Annex D presents some functions of temperature for the thermal and mechanical properties to be used in advanced calculation methods that are not defined. The content of these two annexes is generally considered as not being reliable for design purposes because of the absence of adequate validation by experimental tests. For this reason, there is a need to replace the existing calculation method with tools for the researchers and technicians where the performance-based design approach is preserved.

In the last decade, experimental investigations on masonry elements followed by empirical model development have been carried out [3, 4]. However, data on the behaviour of AAC masonry under fire actions are still limited if compared with those available for clay brick masonry.

Although technical literature provides contributions to the prediction of the mechanical behaviour of masonry panels subject to fire [5], it has been recognized that currently there are no calculation methods which have been calibrated against full scale wall samples.

For this reason, this contribution reports shortly about the indications for an experimental procedure for the determination of the input parameters to be adopted in future advanced calculation models [6]. These parameters would require to be validated by experimental tests on wall panels in accordance with EN 1364 [7] and EN 1365 [8, 9]. After such validation, the calculation models can be adopted to predict the thermo-mechanical behaviour of more complex elements (e.g. walls with openings), parts or the entire building structure.

As stated in the current version of the Annex D of EN 1996-1-2 [1, 2], advanced calculation methods for thermal and mechanical response should be based on the acknowledged principles and assumptions of the theory of heat transfer and structural mechanics, considering the changes of mechanical properties with temperature. The thermal response model should include consideration of the relevant thermal actions specified in EN 1991-1-2 [10, 11] and the temperature dependent thermal properties of the materials. The influence of moisture content and of migration of moisture within masonry may conservatively be neglected. The effect of non-uniform thermal exposure and of heat transfer to adjacent building components may be included where appropriate. The pre-set curves of thermal conductivity, specific heat and density as a function of temperature provided in the current Annex D of EN 1996-1-2 [1, 2] for AAC can be assumed to be valid also for the new tool.

The design values of the material strength are depending on the characteristic value of the strength of the material for normal temperature design to EN 1996-1-1 [12] and from the partial safety factor for the relevant material property, for the fire situation. The effects of thermally induced strains and stresses both due to temperature rise and due to temperature differentials, should be considered.

The constitutive law defined by the equation proposed by Andreini et al. [14] can be used in calculation models of masonry members and for the safety verification. It is important to highlight that the stress-strain model defined in this new equation is intended to be used only to simulate the pre-critical mechanical behavior of the material. The post-critical branch is not considered, this implies that such a material model might lead to loss of truthfulness in the prediction of out-of-plane displacement of a panel but, on the other hand, the overall deformation capacity is conservatively underestimated.

The detailed description is reported in a previous study by Andreini et al. [13]. The procedure adopted for such an experimental determination was mainly aimed to determine the stress-strain relationship in function of temperature. It is worth to be mentioned that no preload was applied to the samples and, therefore, the material creep thermal effect cannot be investigated in such a way.

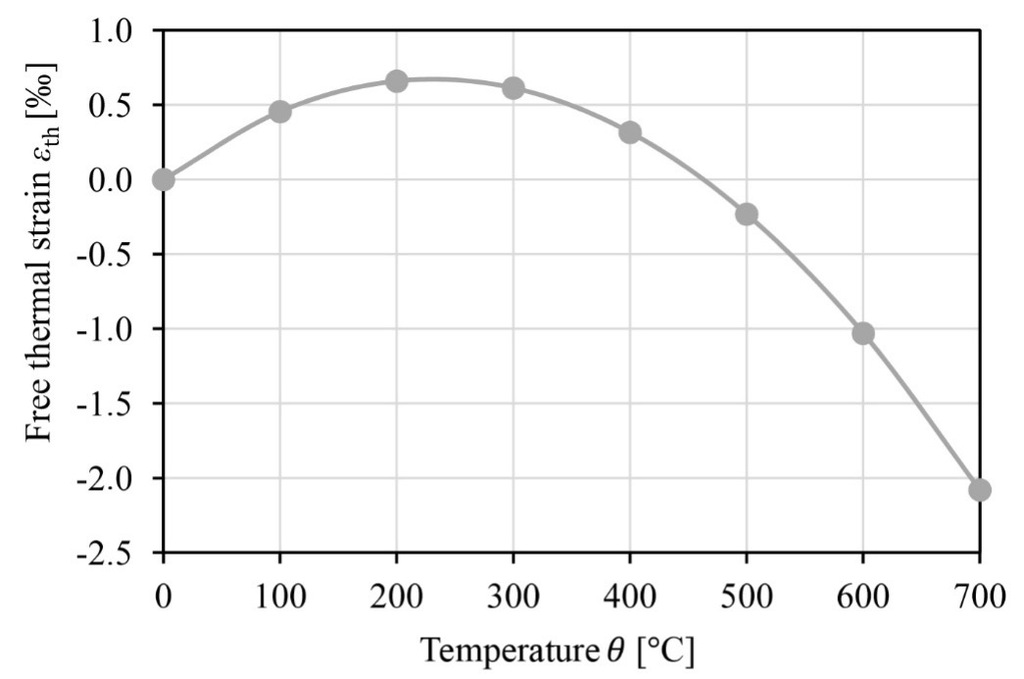
As part of a large experimental campaign of different materials [13] , the AAC samples have been heated and once the test temperature is achieved, the free thermal strain of the sample is measured. Then the compressive strength tests are performed, and the related stress and strain values are calculated. The procedure to test the samples and to determine the mechanical properties are here described [6]. Apart from the mentioned experimental procedure, it has been proposed to provide pre-set stress-strain curves for AAC with a bulk density of 530 kg/m³ based on the results of tests carried out by Andreini et al. [13, 14]. The related stress-strain functions of temperature from the new equation are reported in a previous study [6] . The variation of the free thermal strain is shown in the graph in Figure 2.

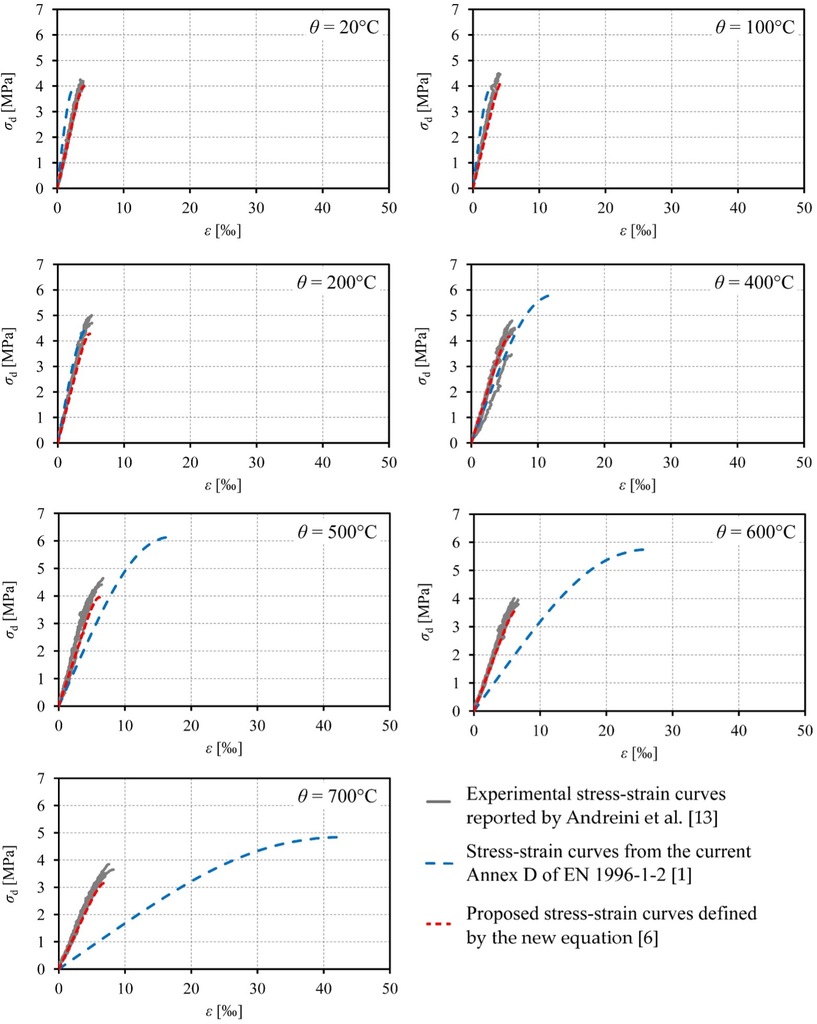
The values of compressive strength of AAC measured during the experimental campaign showed a parabolic trend, increasing up to 200 °C and decreasing for higher temperatures. In general, the samples presented values of the compressive strength almost always lower than those provided by the stress-strain curves drawn in Annex D of EN 1996-1-2 [12]. Analogously, it has been observed that even the ultimate strain of the samples is much lower than the one that can be deducted by the curves of such an Annex.

Figure 3 shows that the stress-strain model of the Annex D of EN 1996-1-2 [1]  fits well the experimental readings for temperatures up to 200 °C. For higher temperatures, such a model predicts much higher values of stress and strain than those observed in the tests; in particular, the strain values predicted by the Annex D model are over 40‰, while the experimental curves do not even reach 7.0‰.

In conclusion, the free thermal strain showed positive values (expansion) up to 460 °C in the tests, while negative values (contractions) were recorded for higher temperatures, as shown in Figure 2. The Annex D of EN 1996-1-2 [1] presents much higher values of the free thermal strain (in contraction), which achieves up to 12‰ around 700°C. According to the authors’ opinion [6], the new curves proposed as result of this study can be suggested as base to be implemented in the new version of EN 1996-1-2.

References

[1]    EN 1996-1-2:2005 (2005) Eurocode 6 - Design of masonry structures - Part 1-2: General rules - Structural fire design, CEN, Brussels.

[2]    EN 1996-1-2:2005/AC:2010 (2010) Eurocode 6 - Design of masonry structures - Part 1-2: General rules - Structural fire design, CEN, Brussels.

[3]    Bošnjak, J., Gambarelli, S., Sharma, A., and Mešković, A. (2020) ‘Experimental and numerical studies on masonry after exposure to elevated temperatures`, Construction and Building Materials, Vol. 230, 116926.

[4]    Russo, S., and Sciarretta, F. (2013) ´Masonry exposed to high temperatures: Mechanical behaviour and properties-An overview´, Fire Safety Journal, Vol. 55, pp. 69–86.

[5]    Andreini, M. and Sassu, M. (2011) ‘Mechanical behaviour of full unit masonry panels under fire action’, Fire Safety Journal, Vol. 46, pp. 440–450.

[6]    Andreini, M. and Miccoli, L. (2022) ’Determination of the stress-strain relationship as a function of temperature for the design of AAC masonry panels subject to fire according to Eurocodes’, International Journal of Masonry Research and Innovation, Vol. 7(6), 589–599.

[7]    EN 1364-1:2015 (2015) Fire resistance tests for non-loadbearing elements - Part 1: Walls, CEN, Brussels.

[8]    EN 1365-4:1999 (1999) Fire resistance tests for loadbearing elements - Part 4: Columns, CEN, Brussels.

[9]    EN 1365-1:2012/AC (2013) Fire resistance tests for loadbearing elements - Part 1: Walls, CEN, Brussels.

[10] EN 1991-1-2:2002 (2002) Eurocode 1: Actions on structures - Part 1-2: General actions - Actions on structures exposed to fire, CEN, Brussels.

[11] EN 1991-1-2:2002/AC:2013 (2013) Eurocode 1: Actions on structures - Part 1-2: General actions - Actions on structures exposed to fire, CEN, Brussels.

[12] EN 1996-1-1:2005+A1:2012 (2012) Eurocode 6 - Design of masonry structures - Part 1-1: General rules for reinforced and unreinforced masonry structures, CEN, Brussels.

[13] Andreini, M., Caciolai, M., La Mendola, S., Mazziotti, L. and Sassu, M. (2015) ‘Mechanical behavior of masonry materials at high temperatures’, Fire and Materials, Vol. 39, No. 1, pp. 41–57.

[14] Andreini, M., De Falco, A. and Sassu, M. (2014) ‘Stress-strain curves for masonry materials exposed to fire action’, Fire Safety Journal, Vol. 69, pp. 43–56.